https://github.com/youngkyu-kim/GappyAE
This repository contains Jupyter notebooks for numerical examples of the paper titled "Gappy Data Reconstruction using Unsupervised Learning for Digital Twin". Note that an open-source FEM solver, MFEM was used to generate training data. Please refer to the paper for more details. Since the size of the training data is large, we do not upload it here. The training data will be provided upon request via email at youngkyu_kim@berkeley.edu.
 Overview
Overview
연구 필요성
디지털 트윈은 실제 존재하는 물리적 대상의 디지털 복제 모델을 지향하나 상대적으로 희소한 측정값 또는 데이터의 누락으로 인하여 디지털 트윈의 성숙도를 물리적 트윈의 수준으로 발전시키는데 제약이 있습니다. 디지털 복제품에 온도 또는 응력상태와 같은 물리적 정보를 실시간으로 동기화시킬 수 있다면, 제품의 제조 공정 모니터링 및 최적화를 통한 고품질의 제품을 효율적으로 생산가능하며, 제품의 운용 기간 동안의 모니터링을 통해 제품의 이상 상태 감지 및 고장 예지를 통한 예방적 유지 보수 서비스를 제공할 수 있습니다. 희소한 데이터만으로 물리적 수준의 디지털 트윈을 구현하기 위해서는 데이터의 특성 및 측정 데이터의 수에 대한 한계를 극복할 수 있는 범용적인 방법으로써 틈이 있는 데이터(gappy data)의 복원 방법론이 필요합니다. 본 과제를 통하여, 비지도 학습을 이용한 비선형 매니폴드 기반 데이터 복원 방법론을 새롭게 제시하여 물리적 상태의 디지털 트윈 구현에 기여하고자 합니다.
연구 목표
본 연구개발과제의 최종 목표는 디지털 트윈에서 실제 존재하는 물리적 대상에 비하여 디지털 모델이 갖는 상대적으로 희소한 측정값 또는 데이터의 누락으로 인하여 발생하는 디지털 트윈의 한계를 극복하기 위하여 틈이 있는 데이터(gappy data)가 주어졌을 때 전체 데이터 예측을 해주는 데이터 복원 알고리즘을 개발하고, 실시간 측정값 기반 상태 예측, 인공지능 학습을 위한 결측치 보정 및 이미지 보정과 같은 영역에 활용하는 것입니다. 기존 방법론으로 적합직교분해(Proper Othogonal Decomposiiton, POD)를 활용한 데이터 복원 방법론인 Gappy POD 방식이 데이터 복원에 활용되고 있습니다. 하지만, Gappy POD 방식은 선형 부분 공간에서 데이터를 예측하기 때문에 Kolmogorov N-width가 큰 특성을 보이는 해를 복원하는 성능에 한계가 존재합니다. 반면에 비지도 학습 모델 기반 비선형 매니폴드를 이용한다면 선형 부분 공간 대비 데이터를 표현하는 능력이 우수합니다. 본 연구를 통해서 비선형 매니폴드를 활용하여 기존 방법론인 Gappy POD 방식이 잘 해결하지 못하는 데이터까지 복원할 수 있는 좀 더 일반화된 알고리즘을 개발하고자 합니다.
 Projects
Projects
연구 내용
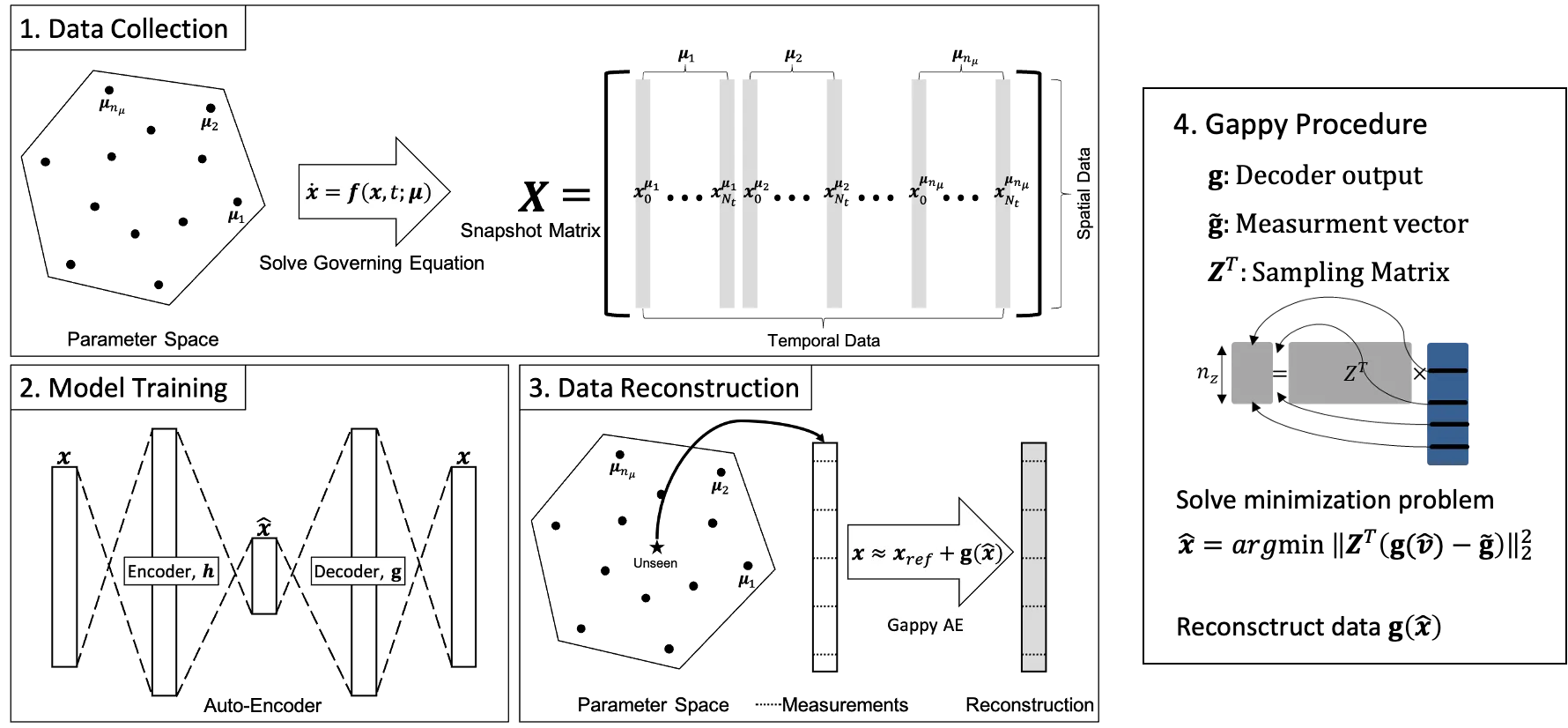
본 연구에서는 오토인코더(Auto-Encoder)를 활용하여 데이터 공간의 특성에 구애받지 않으면서 틈이 있는 데이터(gappy data)를 복원하는 Gappy Auto-Encoder (Gappy AE) 알고리즘을 개발하고자 합니다. 여기서 오토인코더란 인공신경망 기반의 비지도 학습 모델이며 인코더, 디코더, 잠재 공간으로 구성되어 있습니다. 인코더는 입력을 잠재 공간으로 매핑하고 디코더는 입력과 동일한 출력을 합니다. 입력과 출력의 차이를 최소화하는 방식으로 가중치를 조정하여 잠재 공간과 데이터가 존재하는 공간 사이의 비선형 매핑을 학습하게 됩니다.
Gappy AE 알고리즘에서는 학습된 디코더의 예측과 주어진 희소 데이터 사이의 에러를 최소화함으로써 잠재 공간에서의 일반화된 좌표를 계산합니다. 이 일반화된 좌표를 디코더의 입력으로 주면 빈 부분이 복원된 데이터를 얻을 수 있습니다. 또한 본 연구에서 제안하는 Gappy AE 알고리즘을 통해 데이터 측정 위치 및 개수를 데이터 복원 성능 관점에서 제안하여 디지털 트윈 구현에 필요한 센서 배치에 적용하고자 합니다. 특히, 본 연구에서 제안하고자 하는 데이터 복원 알고리즘을 실시간 응용에 적용하기 위해 디코더 구조를 그림 2에서와 같이 얕고 희소한 신경망으로 구성하여 잠재 공간에서 비선형 방정식의 해를 찾는 속도를 증가 시킬 예정입니다.
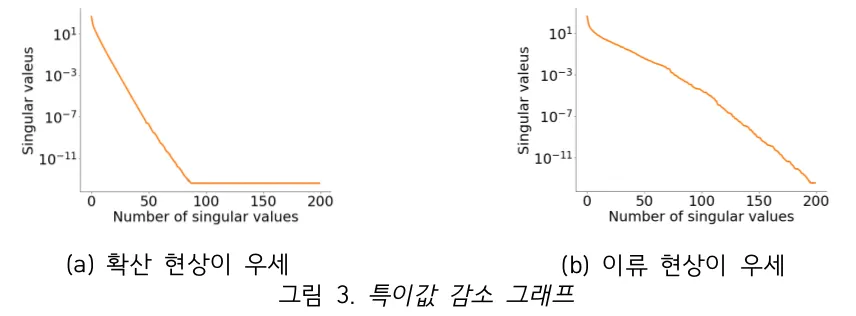
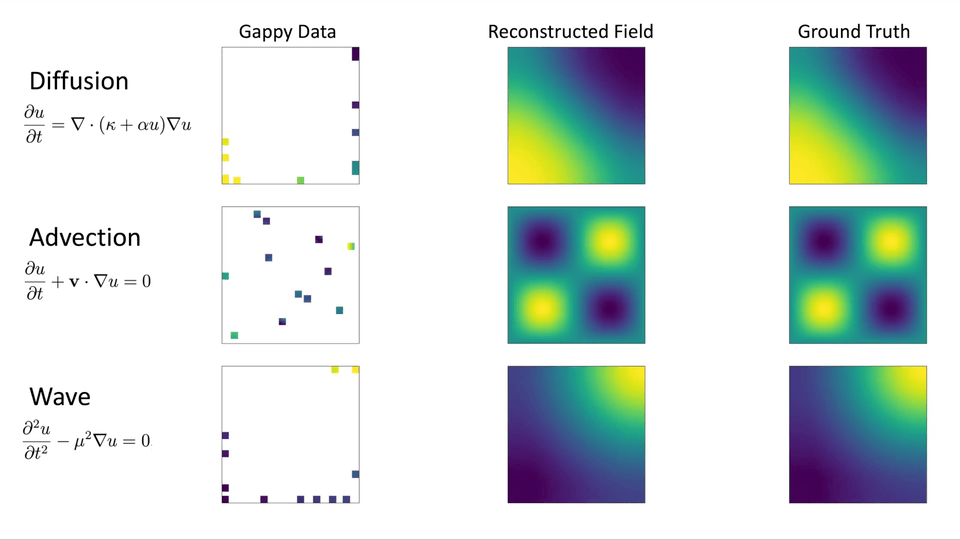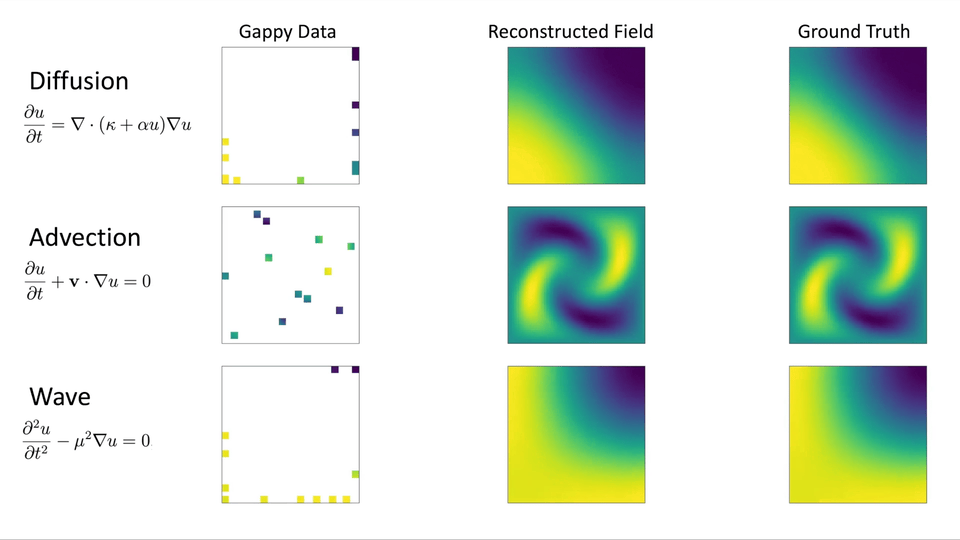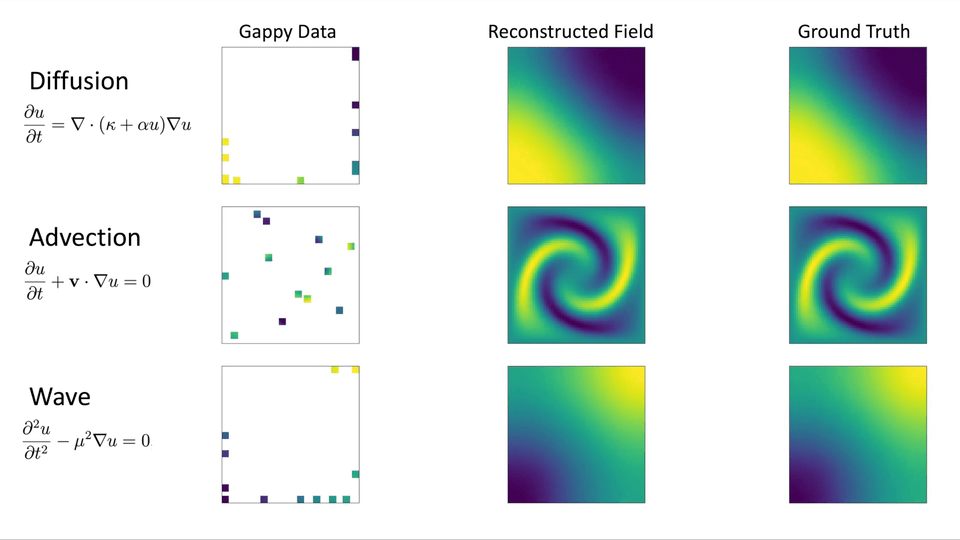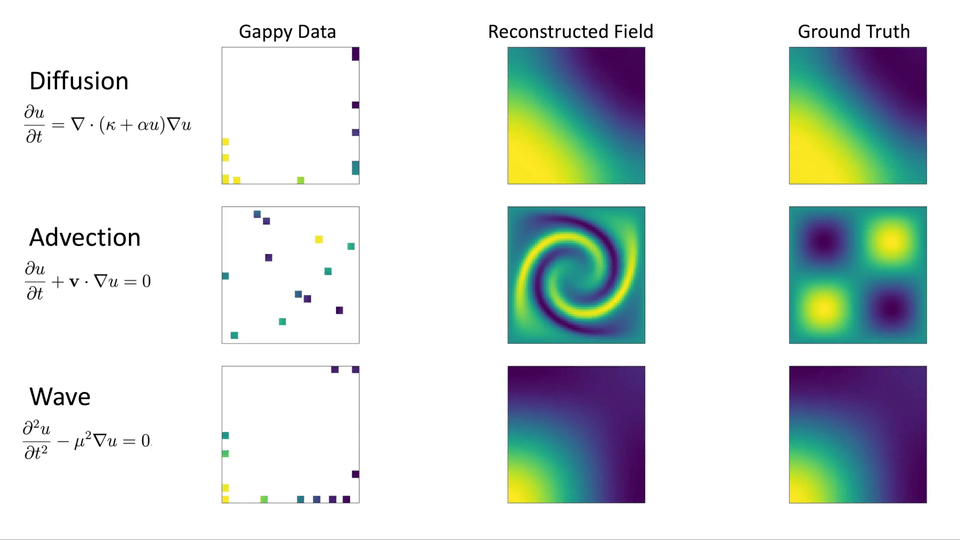
또한 매개변수화된 편미분방정식의 수치해석 결과를 활용하여 Gappy AE 알고리즘 구현 및 성능 테스트를 진행하고자 합니다. 오토인코더 훈련에 사용되지 않은 매개변수에 대한 수치해석 결과의 일부분을 측정값으로 가정하여 나머지 부분의 데이터를 복원할 예정입니다. 아래 그림 3 (a)와 같이 확산이 우세한 지배 방정식의 해 공간은 Kolmogorov N-width가 작으며(특이값 감소가 빠름), 그림 3 (b)와 같이 이류가 우세한 지배 방정식의 해 공간은 Kolmogorov N-width가 크기(특이값 감소가 느림) 때문에, Gappy POD 및 Gappy AE의 성능을 비교하는데 확산 현상을 표현하는 지배 방정식과 이류 현상을 표현하는 지배 방정식을 사용하고자 합니다.
•
희소한 데이터만으로 물리적 수준의 디지털트윈을 구현하기 위한 비선형 알고리즘
•
Decoder의 예측과 희소데이터 간 에러를 최소화하는 잠재공간좌표를 계산하고 이를 활용하여 데이터를 복원
•
개발한 알고리즘을 통해 데이터 복원 성능 관점에서 디지털트윈 구현에 필요한 센서 배치의 효율성을 확보
 Publications
Publications
Table
Search